Livro resgata um fundamento essencial (e quase esquecido) da Matemática

Em 1974, o matemático Michael Freedman começou a estudar um problema muito comum à topologia, uma extensão da geometria. Tratava-se da “Conjectura de Poincaré”, que estabelece que qualquer formato, com algumas característica genéricas, deve ser equivalente a uma esfera.

Poincaré, quando postulou a conjectura em 1904, estava especificamente pensando em formatos tridimensionais, mas matemáticos modernos passaram a considerar todas as dimensões possíveis, aplicando a conjectura em duas correntes distintas: “formatos lisos”, que não trazem cantos ou vértices, permitindo que você crie cálculos a partir de qualquer ponto ou posição; e os “formatos topológicos”, onde há a presença de vértices onde o cálculo é impossível.

Leia também

• Supercomputador suíço calcula novo valor mais preciso de Pi em tempo recorde
• Substância química do cérebro influencia na habilidade matemática
• Físico encontra uma forma de impedir paradoxos na viagem no tempo

É um tipo de fundamento matemático tão complexo e específico que, há quem diga, só é possível entendê-lo se o próprio Freedman estivesse com você, guiando seu estudo. Por causa disso, seu uso nas pesquisas é extremamente raro e, consequentemente, poucas são as pessoas que efetivamente o entendem.

Alguns editores de um novo livro, porém, querem resgatar esse conhecimento, repassando-o adiante por meio da obra “The Disc Embedding Theorem” (“O Teorema da Incorporação de Discos”, na tradução literal). Em aproximadamente 500 páginas, os autores querem tornar o assunto tão divisivo em algo que um estudante universitário possa aprender em apenas um semestre.

“[Com o livro] Não deixamos mais nada para a imaginação”, disse Arunima Ray do Instituto Max Planck de Matemática, que assina a autoria do livro junto de Stefan Behrens (Universidade Bielefeld), Boldizsár Kalmár (Universidade de Budapeste para Tecnologia e Economia), Min Hoon Kim (Universidade Nacional Chonnam, na Coreia do Sul) e Mark Powell (Universidade Durham). “Está tudo devidamente anotado e marcado”.

Outros estudiosos de Poincaré já haviam obtido progresso em formatos de até cinco dimensões, mas Freedman se concentrou na conjectura topológica de quatro dimensões – possivelmente a mais difícil do campo: ela basicamente afirma que todo formato topológico que consiste de uma esfera homotópica tetradimensional é, também, fortemente equivalente a uma esfera comum de quatro dimensões.

Formalmente falando: duas funções contínuas que se movem de um espaço topológico para outro são chamadas de “homotópicas”. A conjectura de quatro dimensões é tida como uma das mais complexas porque, na época em que Freedman a resolveu, as ferramentas usadas por matemáticos não funcionavam muito bem dentro do ambiente restrito tetradimensional.

Para entender como Freedman resolveu esse problema, é importante estabelecermos alguns parâmetros: uma esfera homotópica tetradimensional não é a mesma coisa coisa que uma esfera comum. Aqui, ela é caracterizada pela forma como as curvas desenhadas dentro dela interagem entre si.

No caso da conjectura de quatro dimensões, essas curvas são dois planos bidimensionais. Fica mais fácil de entender considerando a imagem abaixo, onde as curvas de uma única dimensão cruzam dentro de um espaço de duas dimensões:

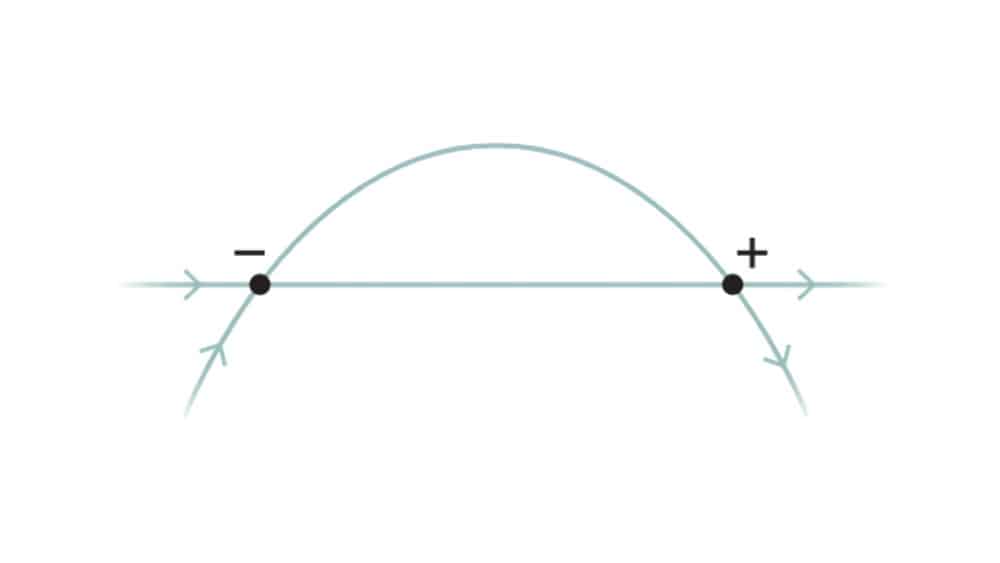
No exemplo acima, ambas as curvas trazem algo chamado “número algébrico de interseção”. Para sabermos qual é esse número, basta assinalarmos o valor de “-1” para todos os pontos cruzados onde a curva está subindo; e o valor de “+1” para os pontos cruzados onde a curva estiver descendo. Como temos um ponto para cada na imagem, então sabemos que o número algébrico é “0”.

Esse mesmo número é característico da esfera homotópica e também da esfera comum, com a diferença de que a esfera comum pode ter suas curvas desenhadas para não se cruzarem em nenhum momento. O número continua sendo “0”, mas sem contabilizar os pontos de interseção posicionados acima.

Aqui, começa o problema resolvido por Freedman: ele precisava mostrar que sempre será possível pegar pares de curvas com número de interseção “0” e “empurrá-las” para longe uma da outra, sem alterar esse número. Se você tem pares de curvas com números de interseção “0” e consegue afastá-los entre si, então você provou que o espaço onde elas estão incorporadas deve ser o de uma esfera comum.

Os estudos do homem levaram sete anos de um quase isolamento social (e você aí, achando ruim os afastamentos causados pela pandemia), onde Freedman não interagiu com praticamente ninguém. Eventualmente, ele conseguiu seu objetivo, mas seu trabalho quase desapareceu quando ele próprio falhou em comprovar que isso era algo “apresentável” em qualquer nível estudantil – ao contrário de outros campos científicos, não há um “corpo de jurados” que julgue trabalhos matemáticos como corretos.

Freedman apresentou suas conclusões para diversas mentes fortes da comunidade, que lhe ajudaram a propagar esse conhecimento, mas para atingir um status mais distribuído, ele precisava de um comunicado por escrito da prova, para que pessoas que nunca o viram antes pudessem ler e aprender por conta própria. Ele nunca fez isso.

Freedman, hoje, trabalha no Station Q, um projeto da Microsoft dentro da Universidade de Santa Barbara, Califórnia, para o desenvolvimento de um computador quântico de capacidades de cálculo topológico: “eu provavelmente não tratei a exposição do material escrito com o cuidado que deveria”, ele disse.

O livro já está disponível nos EUA, mas não tem previsão de chegar em versão traduzida para o Brasil.

Já assistiu aos nossos novos vídeos no YouTube? Inscreva-se no nosso canal!