Quem não gosta de contemplar a beleza de um eclipse lunar como o que ocorreu na madrugada da última sexta, 19 de novembro? Mas você sabia que há mais de 2.200 anos, um grego calculou a distância entre a Terra e a Lua a partir da observação de um eclipse lunar e usando apenas matemática, uma vela e uma moeda?
Leia mais:
- Conheça a “Arp 91”, dupla de galáxias conectadas fotografada pelo Hubble
- Telescópio Hubble acompanha transformação de estrela moribunda
- Nebulosa do Véu: Nasa divulga bela imagem capturada com o telescópio Hubble
Aristarco de Samos foi um astrônomo e matemático grego que viveu entre os anos 310 a.C. e 230 a.C. Teve importantes contribuições na Matemática, e foi o primeiro cientista a propor que a Terra deveria girar em torno do Sol e de seu próprio eixo. Mas sua grande obra foi “Sobre os tamanhos e distâncias entre o Sol e a Lua”.
Não devia ser nada fácil a vida de um cientista naquela época. Mesmo antes da invenção do telescópio, do astrolábio, da internet e do cafezinho, Aristarco se empenhou no cálculo dos tamanhos e distâncias entre a Terra, a Lua e o Sol. Para isso, ele utilizou toda a “tecnologia” disponível, alguma matemática e muita criatividade.
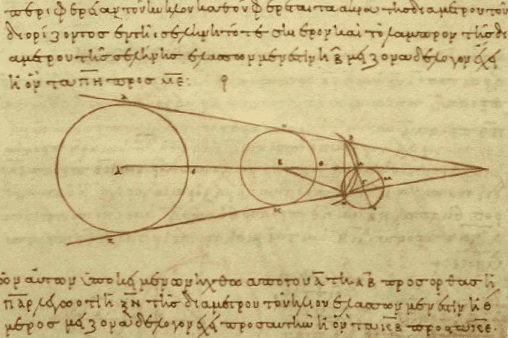
Com uma moeda na mão, Aristarco apontou ela na direção da Lua e a posicionou de modo que ela encobrisse totalmente o astro. Então, mediu a distância entre a moeda e seu olho, que era equivalente a 108 vezes o diâmetro da moeda. Pelo princípio da semelhança entre triângulos, concluiu que a Lua estaria a uma distância de 108 vezes o seu diâmetro. Mas qual seria o diâmetro da Lua?

Para medir o tamanho da Lua, Aristarco observou um eclipse e calculou o diâmetro da sombra da Terra projetada na Lua. Esse cálculo ele fez medindo o tempo em que a Lua demorava para entrar e sair da sombra da Terra. O tempo em que ela leva para entrar na sombra da Terra é o tempo em que a Lua percorre seu próprio diâmetro. E o tempo até ela deixar completamente a sombra, é o tempo em que a Lua percorre o diâmetro dessa sombra.
Assim, Aristarco calculou que a sombra da Terra tinha cerca de duas vezes o diâmetro da Lua. Ótimo. Mas até então, não sabíamos qual o diâmetro da Lua.

Aí, contamos com uma coincidência da natureza. Sol e Lua têm aproximadamente o mesmo tamanho aparente no céu. Os gregos já sabiam disso porque durante os eclipses totais do Sol, a Lua encobria totalmente o Sol por alguns instantes. Então, Aristarco pode utilizar aquela mesma relação de 108 vezes o diâmetro do objeto e considerar que o cone de sombra da Terra se projeta até uma distância de 108 vezes o diâmetro do planeta. Sabendo disso e sabendo o tamanho da sombra da Terra, Aristarco utilizou, mais uma vez, o princípio da semelhança entre triângulos e calculou que o diâmetro da Lua seria cerca de um terço do diâmetro da Terra. Assim, a distância entre Terra e Lua seria equivalente a 36 diâmetros terrestres (que é um terço de 108 vezes o diâmetro da Terra).

Obviamente você esperava que Aristarco lhe desse uma distância em quilômetros. Mas olha, nem o quilômetro existia naquela época (o sistema métrico decimal só passou a vigorar no século XVII), e a humanidade ainda esperaria uns anos até descobrir o diâmetro da Terra. Ainda assim, falta dizer onde entra a vela nessa história.
Pois é. Naquela época também não existiam relógios nem ampulhetas. Então, para medir as durações do eclipse, Aristarco acendeu uma vela e mediu o quanto ela queimava durante cada fase. Considerando que a vela queimava de forma constante, podia converter a medida do comprimento queimado da vela em medida de tempo.

Fica claro a dificuldade para obter medidas precisas com aquela “tecnologia”. Por conta disso, os cálculos de Aristarco não foram tão precisos. A Lua, na verdade, é 3,7 vezes menor que a Terra e está a uma distância de 30 diâmetros terrestres. Mas veja que, mesmo com tanta precariedade, Aristarco se aproximou bastante dos valores reais. Nada mal, considerando que a estimativa anterior era que o diâmetro da Lua seria 72 vezes menor que o da Terra.
E por falar em Terra, poucos anos depois, Eratóstenes, calculou com precisão o diâmetro do nosso planeta, e isso deu valores mais palpáveis aos cálculos de Aristarco de Samos.
Já assistiu aos novos vídeos no YouTube do Olhar Digital? Inscreva-se no canal!


